Gravitation

Digitale Comics
Gute Reise, Mister Newton !
Gibt es im Weltraum Schwerkraft ? Das müssen Mitglieder der Supertroupers in der Inszenierung von « Micromégas » überprüfen, in der Voltaires Riese von einem Planeten zum nächsten flattert wie ein Vogel von Ast zu Ast ...
Teilen Sie diese Episode mit Ihren Schülern
-
Überblick
In dieser Episode diskutieren die Supertrouper über die Theateradaption von Voltaires Erzählung „Micromégas“, während sie in einer Boulderhalle trainieren. Dabei stellen sie die Frage, ob es im Weltraum Schwerkraft gibt, insbesondere im Hinblick auf den Zustand der Schwerelosigkeit eines Astronauten. Sie erkennen, dass die Geschwindigkeit des freien Falls unabhängig von der Masse ist. Aus der Perspektive einer fallenden Person scheinen andere Objekte, die ebenfalls fallen, in der Schwerelosigkeit zu schweben. Dies zeigt, dass Bewegung oder deren Abwesenheit vom Standpunkt des Betrachters abhängt. Dann erkennen die Jugendlichen, dass sich ein schwereloser Astronaut in einer Raumstation von der Erde aus betrachtet in einer Umlauf- oder Orbitalbewegung befindet. Dabei bewegen sich der Astronaut und die Raumstation synchron, obwohl ihre Massen unterschiedlich sind, genauso wie beim freien Fall. Am Ende ihres Stücks integrieren die Supertrouper das historische Gedankenexperiment von „Newtons Kanonenkugel“, um die Ähnlichkeiten zwischen freiem Fall und Orbitalbewegung zu verdeutlichen: Beide Bewegungen können durch die horizontale Geschwindigkeit miteinander in Zusammenhang gebracht werden.
In dieser Episode und dem dazugehörigen Lehrinhalt geht es darum, erste qualitative Argumente für die Existenz von Schwerkraft im Weltraum zu entwickeln: Wenn wir den freien Fall auf der Erde als Ergebnis der Schwerkraft betrachten und die Bewegung der Astronauten im Orbit als „einen gleichen Typ von Bewegung“ wie den freien Fall ansehen, müssten daraus folgen, dass auch die Orbitalbewegung durch Schwerkraft beeinflusst wird. Daher müsste es auch im Weltraum eine Schwerkraft geben!
-
Vorstellungen von Lernenden zu Schwerkraft und Gravitation
Laut Forschungsliteratur zum Physikunterricht ist die Vorstellung, dass es „keine Schwerkraft im Weltraum“ gibt, unter Schülern weit verbreitet (Kavanagh & Sneider, 2006). Sie kann mit anderen verbreiteten Auffassungen zusammenhängen, wie zum Beispiel den folgenden:
- Objekte in der Umlaufbahn haben kein Gewicht, daher wirkt sich die Schwerkraft nicht auf sie aus (=> es gibt also keine Schwerkraft im Weltraum).
- Die Schwerkraft erfordert das Vorhandensein von Luft (=> daher gibt es im Weltraum keine Schwerkraft).
- Die Schwerkraft nimmt mit zunehmender Höhe sehr schnell ab (=> bis es im Weltraum keine Schwerkraft mehr gibt).
Diese Vorstellungen lassen sich mit den in den Medien weit verbreiteten Bildern von Astronauten in Schwerelosigkeit in Verbindung bringen. Da der Begriff Schwerkraft in der Alltagssprache mit dem Phänomen des Fallens in Verbindung gebracht wird, scheint die Tatsache, dass die Astronauten nicht fallen, sondern „schweben“, zu implizieren, dass es im Weltraum keine Schwerkraft gibt, gemäß einer gängigen Argumentation, die sich wie folgt zusammenfassen lässt: „Kein Fall, also keine Schwerkraft“.
Die Ungültigkeit dieser Logik aus Sicht der Physik liegt darin, dass mit dem Begriff der Schwerkraft - oder Gravitationskraft - nicht nur der senkrechte oder waagerechte Fall, sondern auch die Orbitalbewegung im Weltraum erklärt werden kann. Die schwerelosen Astronauten in ihrer Raumstation bewegen sich, vom Erdmittelpunkt aus betrachtet, tatsächlich in einer Kreisbewegung um die Erde.
-
Konzeptioneller Ansatz
Ziel dieser Episode ist es, überzeugende Argumente zu präsentieren, die belegen, dass es im Weltraum Schwerkraft gibt, auch wenn dies zunächst nicht offensichtlich erscheint.
Die anfängliche Logik „kein Fall, keine Schwerkraft“ (für den Astronauten in der Schwerelosigkeit) zu überwinden, bedeutet zu verstehen, wie der Begriff der Schwerkraft auf die Bewegung in einer Umlaufbahn (Orbitalbewegung) ausgedehnt werden kann, die sich optisch sehr stark von einem Fall unterscheidet. Die pädagogische Herausforderung besteht also darin, die Zusammenhänge zwischen freiem Fall und Orbitalbewegung zu verdeutlichen.
Der erste Zusammenhang wird hergestellt, indem man den freien Fall aus der Perspektive des fallenden Körpers betrachtet: Er nimmt seine Situation als Zustand der Schwerelosigkeit wahr, genauso wie es ein Astronaut in einer Umlaufbahn im Weltraum aus seiner eigenen Perspektive tun würde. Eine zweite Gemeinsamkeit (die eine andere Sichtweise der ersten ist) lässt sich durch die Betrachtung folgender Tatsache verdeutlichen: Schwerelosigkeit eines Astronauten innerhalb (oder außerhalb) einer Raumstation bedeutet, dass der Astronaut die gleiche Flugbahn und die gleiche Geschwindigkeit wie die Raumstation hat, obwohl ihre Massen sehr unterschiedlich sind. Diese Tatsache kann mit dem freien Fall von Körpern auf der Erde verglichen werden, wo die Geschwindigkeit bekanntlich nicht von der Masse abhängt (wenn der Einfluss der Luft vernachlässigbar ist). Diese Überlegung stellt die wichtigste Besonderheit des konzeptionellen Ansatzes dar. Obwohl es sich um eine allgemein zugängliche Information handelt, wenn man sich auf die Abwesenheit von Gewicht konzentriert, wird der Zusammenhang dieser Beobachtung mit der Unabhängigkeit des freien Falls von der Masse fast nie deutlich gemacht.
Nachdem in Kapitel 2 diese Gemeinsamkeiten herausgearbeitet wurden, präsentiert Kapitel 3 das historische Schema von Newtons „Kanonenkugel“. In diesem Schema werden die verschiedenen Flugbahnen eines Objekts in Abhängigkeit von der anfänglichen Geschwindigkeit betrachtet. Es zeigt die Kontinuität zwischen freiem Fall und Orbitalbewegung und hilft, die Zusammenhänge zu verstehen. Der senkrechte Fall, der waagerechte Fall und die Orbitalbewegung können als drei Varianten derselben Art von Bewegung betrachtet werden, die mit der Schwerkraft verbunden ist. Dies steht im Gegensatz zur ursprünglichen Annahme, dass Schwerkraft im Weltraum nicht vorhanden ist. Um den Geltungsbereich dieses Konzepts zu erweitern, wird der Begriff „Gravitation“ eingeführt.
-
Historische und erkenntnistheoretische Perspektive
Historische Bezüge
In dieser Episode wird als wichtigstes historisches Element „Newtons Kanonenkugel“ verwendet, das Newton 1685 in „De mundi Systemate“ (veröffentlicht 1728) vorgeschlagen hat. Dieses Gedankenexperiment stellt verschiedene Flugbahnen für den Fall einer Kanonenkugel in Abhängigkeit von deren jeweiliger Geschwindigkeit dar.
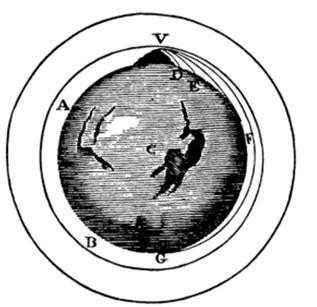
Abbildung 1 – Darstellung von „Newtons Kanonenkugel“ in "De mundi Systemate" (1728) Erkenntnistheoretische Perspektive
Nachdem mehr als 2000 Jahre lang zwischen der irdischen und der himmlischen Welt unterschieden worden war, stellte Newton eine enge physikalische Verbindung zwischen beiden her: Der freie Fall auf der Erde und die Orbitalbewegung im Weltraum können als ein und dieselbe Art von Bewegung verstanden werden, bei der ein und dieselbe Kraft wirkt. Damit wird der Begriff der Gewichtskraft auf die Himmelskörper ausgeweitet: Die Zentripetalkraft, die mit ihrer Umlaufbewegung verbunden ist, ist demnach ihr Gewicht. Die Schwerkraft ist universell.
Das Weltsystem kann so auf eine einzige Weise beschrieben werden, indem dieselbe Kraft die Bewegungen der Erde und des Himmels erklärt. Durch das Zusammenführen von Erde und Himmel begründete Newton das Konzept des Universums.
Nach Newton wurden alle grundlegenden Gesetze der Physik (implizit) als „universell“ betrachtet oder in diesem Sinne erforscht. Der Ansatz dieser Forschung beruhte jedoch auf der Physik selbst: Es war das Ziel, ein grundlegendes Gesetz zu finden, das überall gilt, um darauf basierend anzunehmen, dass auch alle anderen Gesetze universell anwendbar sind.
-
Vorschläge zu verschiedenen Einsatzmöglichkeiten im Unterricht
Voraussetzungen
Eine wesentliche Voraussetzung betrifft den freien Fall. Obwohl das Phänomen sehr häufig vorkommt, haben erste Versuche mit dem Science-Comic im Unterricht gezeigt, dass viele Schülerinnen und Schüler der 10. Klasse sehr erstaunt darüber sind, dass die Fallgeschwindigkeit eines Objekts unabhängig von seiner Masse ist, wenn man den Einfluss der Luft vernachlässigt.
Ihre Fokussierung auf diesen Punkt hat die Aufmerksamkeit von den Informationen abgelenkt, die im weiteren Verlauf der Geschichte kommen und die darauf abzielen, die Fallbewegung mit der Orbitalbewegung zu verknüpfen. Es wird daher dringend empfohlen, im Vorfeld der Unterrichtsstunde auf diese Beobachtung hinzuweisen, sodass sich die Schülerinnen und Schüler auf Kapitel 2 konzentrieren können.
Mögliche Ressource: Video eines Fall-Experiments in einer Vakuumkammer (Brian Cox, Nasa)
LINK zu BBC-Video (Titel des Videos: Brian Cox besucht die weltgrößte Vakuumkammer …)
Video eines Fall-Experiments in einer Vakuumkammer (Brian Cox, Nasa) Zum Einstieg: Was ist die wissenschaftliche Fragestellung?
Nach einer ersten individuellen Lektüre des Comics durch die Schülerinnen und Schüler kann es sinnvoll sein, zunächst das physikalische Problem zu erläutern, das im ersten Kapitel auftaucht: „Gibt es Gravitation im Weltraum oder nicht?“ Dazu können die Schülerinnen und Schüler nach der Position der verschiedenen Figuren zu dieser Frage und nach deren Argumenten befragt werden.
Vom Science-Comic zur Physik: gemeinsame Lektüre mit Fragen.
Nach einer individuellen Lektüre kann eine gemeinsame Lektüre mit einer Videoprojektion des Comics angeboten werden, deren Tempo von der Lehrkraft gesteuert wird. Hier können dann Fragen zu bestimmten Schlüsselszenen gestellt werden, wie zum Beispiel zu folgenden:

Bildunterschrift: Begey & Govin, Stimuli Eds 2023. Ziel dieser Frage ist es, den Zusammenhang zwischen der Unabhängigkeit des freien Falls von der Masse und der Schwerelosigkeit herzustellen.
Antwort: Die Geschwindigkeit ist gleich, da diese im freien Fall nicht von der Masse abhängt.

chapter 3, p13 Mit dieser Frage wird das Verständnis der Abhängigkeit vom Beobachtungsstandpunkt bei der Beschreibung von Bewegung getestet.
Antwort: Er kann in Bewegung sein, wenn man ihn von einem anderen Standpunkt aus betrachtet.

Die Frage nach der Masse soll das Bewusstsein dafür schärfen, dass es einen großen Unterschied zwischen dem Astronauten und der Raumstation gibt.
Die Fokussierung auf dieses Merkmal kann helfen zu erkennen, dass die Bewegung dieselbe ist, obwohl die Massen sehr unterschiedlich sind, so wie die Schwerkraft.
Antwort: Mehr als 400 Tonnen!

Antwort: An ein Merkmal des freien Falls: Die Fallgeschwindigkeit ist gleich, unabhängig von der Masse.
Von der Physik zum Science-Comic
Nach der Interpretation der Szenen kann der umgekehrte Ansatz gewählt werden: Lassen Sie die Schülerinnen und Schüler allgemeine physikalische Aussagen mithilfe bestimmter Bilder aus dem Comic illustrieren. Es ist auch möglich, sie explizit die Gemeinsamkeiten zwischen Fall und Orbitalbewegung verbinden zu lassen. Hier ein Beispiel für eine Übung (bearbeitbare Version unten).

-
Ergänzende Materialien
-
Potenzielle Unterrichtssequenz
Vorschlag 1: Unterrichtssequenz mit zwei Einheiten
- Erste Unterrichtseinheit (1h)
Individuelle Lektüre (5 Minuten)
Nach einer ersten individuellen Lektüre des Science-Comics durch die Schülerinnen und Schüler kann es sinnvoll sein, zunächst das physikalische Problem zu erläutern, das sich im ersten Kapitel stellt, indem man zum Beispiel die Meinung der verschiedenen Figuren zu dieser Frage und deren Argumente abfragt.
Fragen zu Kapitel 2 (20 Minuten).
Ein wichtiger Schritt bei der Arbeit mit dem Comic im Unterricht ist es, die Schülerinnen und Schüler auf zentrale Szenen aufmerksam zu machen, die eine Reflexion erfordern, um die physikalischen Konzepte zu verstehen, die zur Lösung der Ausgangsfragestellung beitragen.
Dies betrifft insbesondere die beiden Perspektivwechsel, die in Kapitel 2 dargestellt werden: Der Fall aus der Sicht „von innen“ (S. 8) und der Zustand der Schwerelosigkeit aus der Sicht „von außen“ (S. 46).
Ein Beispiel für eine geeignete Fragestellung findet sich in Dokument A unten.
Nachdem die Szenen interpretiert wurden, kann auch der umgekehrte Ansatz verfolgt werden: die allgemeinen physikalischen Konzepte durch spezifische Bilder aus dem Comic zu illustrieren. Dabei können die Ähnlichkeiten zwischen der Fallbewegung und der Orbitalbewegung hervorgehoben werden, wie beispielsweise in Dokument B unten vorgeschlagen.
Arbeit mit den Dokumenten A und B (20 Minuten).
Nachdem diese Gemeinsamkeiten identifiziert wurden, stellt sich die Frage nach ihrer Erklärung: Wie ist es möglich, dass diese scheinbar unterschiedlichen Bewegungen dieselben Merkmale aufweisen? Das in Kapitel 3 beschriebene Gedankenexperiment der „Newtonschen Kanonenkugel“ hilft dabei, die Kontinuität zwischen diesen verschiedenen Bewegungen zu verstehen und ihre Gemeinsamkeiten zu begründen. Der Buchauszug in Dokument A oben bietet eine originelle Interpretation dieses Konzepts. Es ist möglich, dass den Schülerinnen und Schülern der Zusammenhang zwischen den einzelnen Elementen zu diesem Zeitpunkt noch nicht vollständig klar ist. Daher könnte eine explizite Verknüpfung notwendig sein. Dokument B bietet einen kurzen Überblick und erläutert insbesondere den Unterschied zwischen den Begriffen „Schwerkraft“ und „Gravitation“. Es weist darauf hin, dass die Orbitalbewegung mit der Gravitation in Verbindung gebracht werden kann. Damit ist es nur noch ein Schritt, bis die Schülerinnen und Schüler ableiten können, dass es im Weltraum tatsächlich Gravitation gibt, womit die Antwort auf die Ausgangsfrage gegeben wird.
- Zweite Unterrichtseinheit (1 h)
In der zweiten Unterrichtseinheit arbeiten die Schülerinnen und Schüler daran, den Gedankengang zu nachzuvollziehen, der zur Lösung der Ausgangsfragestellung führt. Nach einer erneuten Lektüre der Comic-Episode erhalten sie folgende Anweisung: „Viele Menschen glauben, dass es im Weltraum keine Schwerkraft gibt, insbesondere wenn sie an die schwebenden Astronauten denken. Verfassen Sie einen kurzen Text, der auf dem Comic und der vorherigen Stunde basiert, um die Menschen davon zu überzeugen, dass es im Weltraum trotz der Schwerelosigkeit der Astronauten tatsächlich Schwerkraft gibt.“
Da diese Aufgabe für die Schülerinnen und Schüler herausfordernd sein kann, könnte es notwendig sein, verschiedene Stufen der Unterstützung anzubieten.
Credits
-
Szenario
Lau Bergey und Valentin Maron
-
Storyboard
Barbara Govin
-
Illustration
Barbara Govin und Aline Rollin
-
Entwicklung von Computersoftware
Clément Partiot
-
Webdesign
Gauthier Mesnil-Blanc
-
Übersetzen
Heinke Wagner
-
Forschung im Bereich der wissenschaftlichen Bildung in der Physik
Valentin Maron
-
Produktion
Stimuli Eds
-
Veröffentlichung
November 2024
-
ISBN
978-2-9593956-1-1

